by Bruce J. Lindbloom
Note: I was notified by Dr. János Schanda and Todd Newman on 3 April 2003 that the CIE 15.316 and the CIE Standard on CIELAB will implement this fix (i.e. using rational rather than decimal values for these constants).
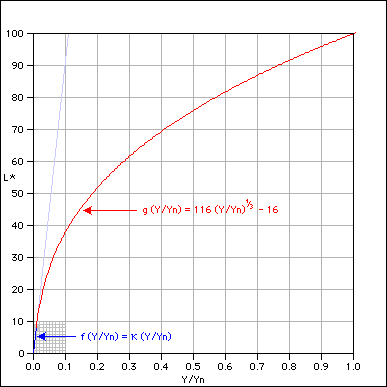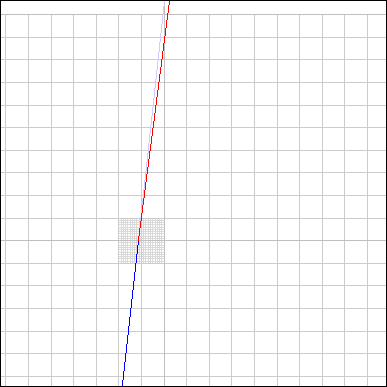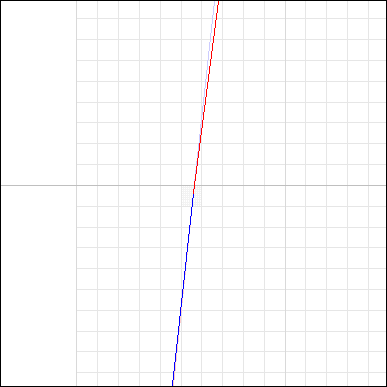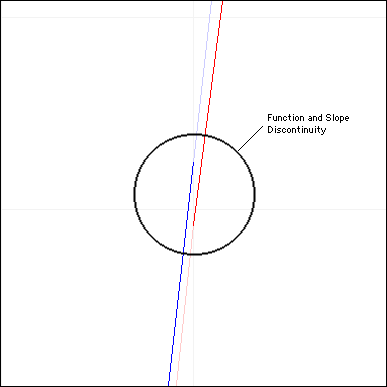
The CIE equation for mapping relative luminance ($Y/Y_n$) into lightness ($L*$) is composed of two separate functions, $f()$ and $g()$:
$$L* = \cases{ f(Y/Y_n) & \text{if }Y/Y_n \leq \epsilon \\ g(Y/Y_n) & \text{if }Y/Y_n \gt \epsilon }$$where
$$f(Y/Y_n) = \kappa Y / Y_n$$ $$g(Y/Y_n) = 116 {(Y/Y_n)}^{1/3} - 16$$The two functions are "grafted" together at $\epsilon$, which I will call the junction point. The two constants, $\kappa$ and $\epsilon$ are given by the CIE standards [Supplement No. 2 to CIE Publication No. 15 (E-1.3.1) 1971 / (TC-1.3) 1978] as:
$$\kappa = 903.3$$ $$\epsilon = 0.008856$$Substitution of these values into equations [2] and [3] shows that there is a discontinuity at the junction point:
$$f(\epsilon) = 7.999624800$$ $$g(\epsilon) = 7.999591993$$This break may be seen by taking a closeup view of the junction point of the two functions. In the following animation, $f()$ is drawn in blue and $g()$ is drawn in red. As we zoom into the junction point, the discontinuity becomes apparent:

As may be seen, not only is the function discontinuous, it is also non-monotonic, which makes it not invertable in this region. What about the slopes at the junction point? We may compare them by taking the first derivatives of equations [2] and [3]:
$$f'(Y/Y_n) = \kappa$$ $$g'(Y/Y_n) = (116{(Y/Y_n)}^{-2/3})/3$$Again making the substitution shows that the slopes are also mismatched at the junction point:
$$f'(\epsilon) = 903.3000000$$ $$g'(\epsilon) = 903.3270068$$If we wish to find modified constants $\hat \kappa$ and $\hat \epsilon$ that provide both function and slope continuity, we must match the functions and their first derivatives at the junction point:
$$f(\hat \epsilon) = g(\hat \epsilon)$$ $$f'(\hat \epsilon) = g'(\hat \epsilon)$$which using equations [2], [3], [8] and [9] becomes
$$\hat \kappa \hat \epsilon = 116 {\hat \epsilon}^{1/3} - 16$$ $$\hat \kappa = (116{\hat \epsilon}^{-2/3})/3$$Solving for the constants $\hat \kappa$ and $\hat \epsilon$ shows that their values may be exactly represented by rational numbers:
$$\hat \kappa = 24389 / 27$$ $$\hat \epsilon = 216 / 24389$$Using these values in place of the published CIE values gives perfect function and slope continuity at the junction point:
$$f(\hat \epsilon) = g(\hat \epsilon) = 8$$ $$f'(\hat \epsilon) = g'(\hat \epsilon) = \hat \kappa$$The CIE's decision to represent these constants as decimal values was an unnecessary approximation that introduces both function and slope discontinuities.
If you examine the CIE equations for conversions between XYZ and Lab, you will find the constant 7.787. By extending the above analysis into these equations, you will find the exact value of this constant to be the rational number $(\hat \kappa / 116)$.
By using the above values for $\hat \kappa$ and $\hat \epsilon$ you will fix function discontinuities, non-monotonicities, inversion failures and slope discontinuities that are present in the published CIE conversions among XYZ, Lab, LCHab, Luv and LCHuv.